Image Segmentation

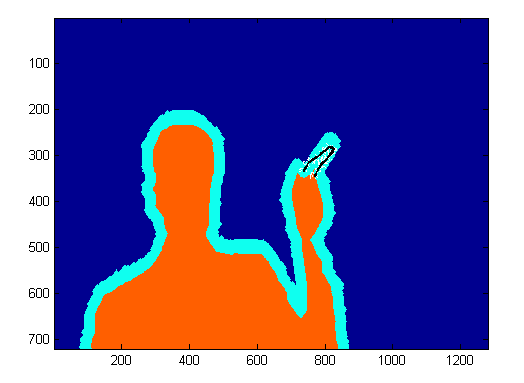
Jed Chou and Anna Weigandt The image segmentation problem is the following: given an image, a vector of pixels each with three associated red, green, and blue (RGB) values, determine which pixels should belong to the background and which should belong to the foreground. For example, in the following picture, the pixels which make up the dog should belong to the foreground, and the pixels making up the wood planks should belong to the background.

maggie
In 2004 Rother, Kolmogorov, and Blake introduced one solution to the image segmentation problem, an algorithm called GrabCut. Roughly, GrabCut works by forming a weighted graph from the pixels, defining an energy or cost function from this graph, and then finding a cut of the graph (an image segmentation) which minimizes the energy function. This minimum cut should in theory yield a good demarcation between background and foreground. We describe the steps in more detail below: First the user specifies an initial segmentation by drawing a rectangle on the image. Everything outside the rectangle is labelled “background” and the pixels inside are labelled “unknown”. Later the user may also mark certain pixels as foreground. A partition of the pixels into three components, foreground, background, and unknown, is called a trimap. Using this initial segmentation, GrabCut creates two Gaussian mixture models (GMMs), one for the background and one for the unknown. A graph is then formed with one node for each pixel and a set of edges connecting neighboring pixels. Each node is assigned a weight based on the GMMs. Each edge, say the edge between node A and node B, is assigned a weight based on the difference between the color intensities at A and at B. An energy function is defined: E=U+V, where U depends on the node weights and V depends on the edge weights. Some algorithm, such as MaxFlow or MinCut, is used to compute the minimum. The minimum energy state should correspond to a good segmentation. GrabCut works very well for many images, but it is sensitive to the initial trimap. In the pictures below, two different trimaps of the same image yield very different results.

mat
In one case, a rectangle is drawn around the dog and in the other, a more detailed outline of the dog is specified. For this image, a simple rectangle around the dog doesn’t provide GrabCut enough information to find a good segmentation. GrabCut, as it was first introduced, does not allow the user to draw a non-rectangular shape for the initial trimap, but it can fix the type of problem shown above by taking additional user input. Our task is to modify GrabCut so that it makes good cuts automatically in such cases, without requiring any additional input beyond the initial rectangular trimap.

Summary

First we studied the grabCut algorithm and some general theory of image segmentation; we also played with some implementations of the grabCut algorithm to get a feel for how it worked. Anna wrote her own implementation of grabCut in matlab based on Gaussian Mixture Models which would take as input an image along with a manually-drawn matte and spit out a segmentation of the image into foreground and background. Our first goal was to get a clean segmentation of the dog picture shown above. Over the weeks we experimented with the dog picture by adjusting the algorithm parameters and we also discussed ways to extract more information from the color data to enhance the performance of Anna’s implementation. We added several matlab functions to do this. In the dog picture above, the problem mostly seemed to be that cutting along the long, upside-down U-shape between the dog’s hind legs and front legs was more expensive than cutting along the shorter distance spanned by a straight line from the bottom of the hind legs to the bottom of the front legs. We suspected that we needed to make it easier to cut along the this upside-down U-shape by decreasing the neighborhood weights along that arc. However, it wasn’t enough to just manually adjust the neighborhood weights–we wanted a way to automatically adjust the neighborhood weights so that such problems wouldn’t occur for other images. So our problem was to figure out which neighborhood weights to adjust and how to adjust them. First we tried using the directionality of the color data. The intuition was that if the colors in a subset of the image were running along a particular direction, then there should be an edge along that direction in the subset of pixels. We tried to capture the directionality in the color data by calculating the covariance matrix over small square windows of the image (the variance-covariance matrix of the variables X and Y where X was a vector consisting of the differences in color intensity in the horizontal direction and Y was a vector consisting of the differences in color intensity in the vertical direction). We then computed the spectrum of the covariance matrix centered at each pixel in the image. If the absolute value of the largest eigenvalue of the matrix was much greater than the absolute value of the smaller eigenvalue (which indicates a strong directionality along the direction of the corresponding eigenvector in that particular window), and also the largest eigenvector was almost horizontal or almost vertical, then we would decrease the corresponding horizontal or vertical neighborhood weight proportionally to the ratio of the eigenvalues. In theory this would make it less expensive to cut along the edges in the image. To check if the code was picking up directionality properly, we placed a vector field over the image where the vector at a pixel p was the eigenvector of the largest eigenvalue of the covariance matrix centered at p. Though the vector field seemed to capture the directionality properly, tweaking the edge weights in this way seemed to have little effect on the output of the algorithm: the large piece of wood flooring between the dog’s legs was still being categorized as foreground, even after we greatly magnified the adjustments to the edge weights based on the ratio of eigenvalues.

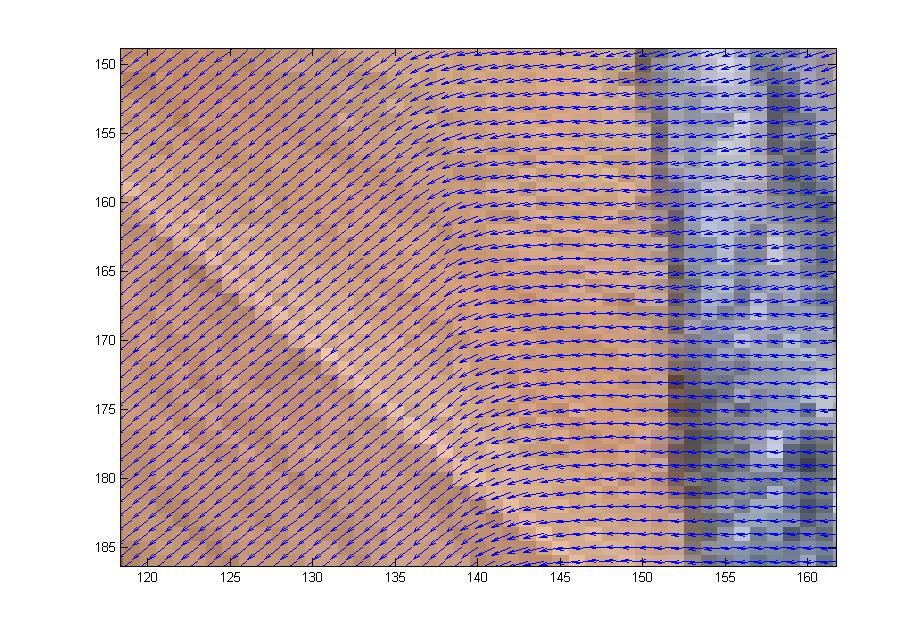
directionality
We then examined the the average node weight and the average neighborhood weight and found that the neighborhood weights were about 10^-5 times smaller than the node weights. This led us to think about adjusting the node weights instead. When we changed the number of components in our Gaussian mixture model to one instead of five, we obtained a clean segmentation of the dog from the background as shown below. For images in which colors are relatively uniform, this approach probably works well. Next we examined a sequence of images from Personify in which a person’s finger was improperly assigned to the background. The problem was similar to the one we encountered for the dog picture: it was too expensive to cut along the outline of the finger rather than across it. We tried ajusting the number of Gaussian components to no avail, so again we tweaked the edge weights.

blocktest
To attempt simplify the problem, we created noisy images of two rectangles sitting atop each other as shown above. However, the set of test images was not reflective of the finger situation. Given a trimap designating the upper rectangle as unknown, grabcut segmented the foreground from the background for all test images.

We next experimented with modifiying select node and neighborhood weights on the finger image. We manually marked certain pixels of the finger of the test image and adjusted the weights so that the selected pixels were forced into the foreground. This strategy only ensured the selected pixels were placed in the foreground. It failed to pull the rest of the finger into the foreground.

trimap
The second strategy seems more promising. We marked a band of pixels around the finger. We then adjusted those pixels by multiplying by some constant, c. Very low values of c, around the order of c=.01, ensured the finger was pulled into the foreground. Marking fewer pixels, near the end of the finger, sometimes was effective, but often would result in portions of the finger being lost. The current direction of work is to experiment with the selection of marked pixels.